Notes
The natural frequency of vibration of structures estimated under
Vibration > Free vibration assumes that damping is not present
and no external force is acting on the structure. In reality, some
form of damping and external forces are present in many MEMS
devices. In many cases MEMS sensors will be subjected to time
varying forces with constant amplitudes like electrostatic
force and its response to such external loads needs to be
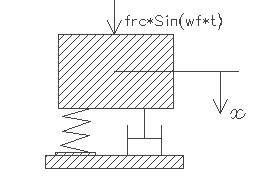
understood. When a spring mass system representing the MEMS device
is subjected to a harmonic excitation as shown, the applied force
varies harmonically with amplitude 'frc' and radial frequency
'wf'. Based on the initial conditions including displacement and
velocity of the mass, it will undergo a transient response
immediately after it starts to vibrate. But as time becomes large,
it assumes a steady state response which will be independent of the
initial conditions. Only steady state vibrations are examined here
and assumes that time is large so that transient response can be
neglected.
This design interface can be used to estimate the resonance frequency, amplitude of vibration and phase lag. The frequency of forced harmonic vibration will be the same as forcing frequency. The resonance frequency is dependent on the natural vibration frequency and damping. When the damping is very small, the resonance frequency is nearly equal to the natural vibration frequency. The vibration amplitude is strongly dependent on damping, the excitation frequency and the properties of the spring mass system. The vibration amplitude is highest when the driving frequency is near the resonance frequency and should be avoided in most cases. When the damping ratio is equal to 0.7, the peak in the amplitude frequency curve nearly disappears and that allows a wide range of excitation frequency to be applied which will not make any change to the vibration amplitude. Hence a damping ratio of 0.7 is known to give a wide bandwidth and is often referred to as the optimum damping condition.
The free vibration frequency is as estimated for the various structures under Vibration > Free vibration. If the damping ratio for air damping is not available it could be estimated using the design forms under Vibration > Damping for a given air gap distance. If spring constant is not known it can be calculated under Mechanics > Structures.
The resonance frequency is estimated for the under damped case (dmp < 0.7) only. There is a phase lag in the vibration of the system with respect to the driving force depending on the damping ratio, the excitation frequency and natural frequency of vibration. If the amplitude of vibration is known, dividing it by the static displacement of the mass which is frc/k will give the relative amplitude.
The plot shows relative amplitude of vibration of the system for a range of driving frequency above and below the natural frequency of the system for the given damping ratio. When the damping is slight (dmp < 0.7), the maximum relative amplitude obtained from the curve is equal to the Quality factor or Q-factor of the system. This maximum amplitude happens also at the resonant frequency. Using the cross hair tool, the resonant frequency, the Q factor and the amplitude of vibration of the system can be estimated from the graph.